PhiloDream

Категорический силлогизм (или просто: силлогизм) - это дедуктивное умозаключение, в котором из двух категорических высказываний выводится новое категорическое высказывание. 1

Логическая теория такого рода умозаключений называется сил-логистикой.

Она была создана еще Аристотелем и долгое время служила образцом логической теории вообще.

В силлогистике выражения «Все . есть .», «Некоторые есть .», «Вс не есть .» и «Некоторые . не есть .» рассматриваются как логические постоянные, т.е. берутся как единое целое. Это не высказывания, а определенные логические формы, из которых получаются высказывания путем подстановки вместо многоточий каких-то имен. Подставляемые имена называются терминами силлогизма[2].

Существенным является следующее традиционное ограничение: термины силлогизма не должны быть пустыми или отрицательными.

Примером силлогизма может быть:

Все жидкости упруги.

Вода - жидкость.

Вода упруга.

Понятия, входящие в состав силлогизма называют его терминами. Большой термин – предикат заключения, посылка, его содержащая – большая посылка (пишется в первой строке силлогизма); Малый термин – субъект заключения, посылка его содержащая – малая посылка (пишется во второй строке); средний термин – общее звено посылок – общее понятие, объединяющее обе посылки (выпадающее в заключении):

Справедливость (P) предусматривает ответственность за поступки (M).

Доброта (S) не требует ответственности (M)

Доброта (S) несправедлива (P).

Положение среднего термина определяет четыре типа построения (фигуры) простого категорического силлогизма, каждый из которых должен соответствовать своему формальному правилу вывода:

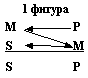
Большая посылка должна быть более общей, меньшая утвердительной. Ее формула (модус) последовательности посылок и следствия AAA, EAE, AII, EIO – любые другие комбинации ошибочны

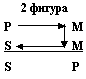
Большая посылка должна быть более общей и одна из посылок, а так же, заключение – отрицательным: AEE, AOO, EAE, EIO

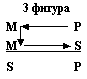
Меньшая посылка должна быть утвердительной, а заключение – частным: AAI, EAO, IAI, OAO, AII, EIO

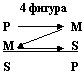
Не дает общеутвердительных заключений. Если большая посылка утвердительная, то меньшая должна быть общей. Если одна из посылок отрицательна, то обшей должна быть большая посылка: AAI, AEE, IAI, EAO, EIO.

Проверку правильности вывода легко провести, заменив смысловые значения символами (A, I, E, O) и определив тип фигуры. Так, суждение «Нечеткие и не лаконичные суждения не следуют логике в должной степени» можно представить в виде силлогизма:

A Вся логика (P) является необходимой для правильной формулировки суждений (M).

O Некоторые суждения (S) формулируются не вполне правильно (M)

O Некоторые суждения (S) не вполне соответствует логике (P).

Где большая посылка общая (в данном случае, общеутвердительная), а другая (малая) и заключение – отрицательные (в данном случае частноотрицательные), из чего видно что, это умозаключение имеет структуру AOO и соответствует правилу второй фигуры. Таким образом, полученный вывод истинен.